一個A/D 的系統應用問題（續篇-範例版）

對於這個A/D 的First Order Filter 的系統應用問題，在此將引用到一個簡單的應用來看實際的範例。

常用系統應用問題就是藉由VR 旋鈕來設定一些系統參數改變，像是設定馬達轉速或LED 調光等。

在我這個範例就是利用簡單的旋鈕來設定機車點火轉速模擬器，藉由VR旋鈕來設定機車引擎轉速。

我之前也是利用連續讀十次再加以平均的作法來作的，沒有錯啊，這樣子當然有一定的濾波效果，

但是在這種高壓點火不可避免會產生電磁波干擾源的惡劣環境中，

總是偶爾還是會發生設定轉速突然跳動一下的現象。原來也不以為意，但總覺得很不舒服，

而且客人也會覺得您這個東西好像還是有點怪怪的？！是不是那邊還有問題？！

搞不清楚是您轉速模擬器有問題呢？！還是您的點火控制器有問題？！

（因為點火控制器是依據轉速模擬器來決定點火進角的！）

好了，我就來看這個實驗結果：

下圖就是這兩種作法

（一種是連續讀十次在平均的作法；另一種是利用我數學上First Order Filter作法！）

（圖一）

First Order Filter 是每一個間隔時間（15mSec）都會讀取A/D ，然後馬上計算濾波後的工程值。

而連續讀十次的是要讀取十次後，才能計算一次工程平均值。

（至於要不要加入誤差過大的判斷式？！您自個兒可以自行決定要不要加入程式處理。）

我們發現：我們大部分讀到的 A/D 是 176 ，但偶爾也會讀到 175 ，

這一點有可能是高壓電磁波干擾，也有可能是硬體電路的問題，

（當然在硬體上我已經有加一般RC 濾波電路了！）

這種簡單的 ± 1 的變化應該還算是正常的吧！如果依據誤差判斷式而言應該也是合理的。

另外中間偏下那個 "ADC = 176 ,RPMSET =" 也就是我們取平均方式的結果。

看起來是一樣的，所以，沒有人跟您說：不能用取平均的作法啊。

但是，我們再來看下一張讀到值的圖示：

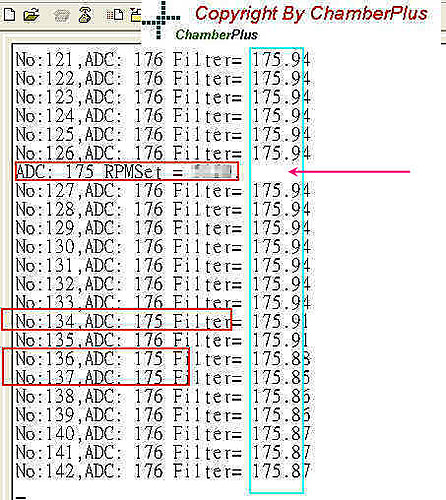（圖二）

我們發現：當我讀到那個平均值的作法時，有可能隨著外在諸多環境影響之下，

（電磁波干擾？電源電路？）

可能讀到  175 的頻率與次數變多一點點之後，我們取平均的算法，就真的會變成 175 了。

但我們若從一階濾波器的結果來看：他還是維持在 176 ，（其實應該是 175.8~175.9 ）

這問題以數學眼光來看：一階濾波器本來就會造成些許的LAG ，這是他數學上的現象。

但我們從工程來看：他也算是合理可以接受的，這跟我們在硬體電路上採用RC 濾波也是一樣的。

所以，我們很明顯就發現這兩種作法有其不同的結果。那您會跟我說：只差 ± 1有差嗎？！

因為若我們是利用 8 Bits A/D 的話，就是差 1/256 ，

那如果我RPM 的設定範圍是0 ~20,000 RPM 的話。

不好意思，這個± 1 剛好可能會放大造成 ± 80 RPM 的變化跳動，

您說：人家現在許多工業用的高速加工機的馬達動不動是幾十萬轉的，這個± 1 您說會差多少？！

如果是那一種遙控飛機用的無刷馬達控制的話，他的馬達RPM 也是上萬轉的...

這個± 1 的誤差跳動應該也不小吧！又螺旋槳再不穩定旋轉之下，當然就是影響他的飛行穩定度啊。

過去有許多人在控制馬達時，或是想拿一些低階的MCU玩馬達控制時，

總以為好像是我後面那些PWM 控制回路或是Gate Driver一些可能有問題？

很少人會去懷疑控制輸入信號參數或是為了降低這個輸入參數的變動值，只好採用更高檔的A/D ，

譬如從8 Bits A/D 改成 12 bits A/D...那怕他的應用只要 8 Bits 就夠了。

（又是個數學功力不夠，又要『牽拖』MCU 效能不佳的案例了，

12 bits A/D 又比 8 Bits A/D 又貴又不好找！）

所以，我們從這個案例結果來討論一些結論：

* 以連續讀再取平均值的作法，沒有錯，他當然是可以接受的，

但這個中間好像會牽涉到所謂機率問題。因為，如果您每次讀的時候，

剛好都發生A/D 跳動時，次數一增加就會影響您平均值的計算了。

而這個跳動值，可能還在您程式可以接受的誤差範圍內。

（這一點好像跟工程數學學理有點無關了...這是理論與實際會碰到的現象是不同的！）

*以一階濾波器的作法，他的程式的數學運算量會增加，

因為每讀一次A/D 值就要呼叫一階濾波器運算式，

但是他的結果看起來是相對比較穩定多了。

也是因為會增加MCU 程式運算量，我們才要發展一個簡單容易的一階濾波器8 bits 運算式啊。

使得這個副程式可以套用到一般簡單的MCU 裡面，而不用過度依賴選用特定的MCU，

這一點對於那些要選用MCU 來玩市場比較大的玩具無刷馬達應用市場是比較正面有意義的。

也對於我們自己在選用MCU 時，可以因應不同的系統需求而調整MCU 的選用。

（所以，如果有賣MCU 的業務跟您說：我們家的MCU 比較特別啊...有別人所沒有的特別功能時，

想一想：真的是如此嗎？！那到底是他的MCU 比較好呢？！還是您自己系統應用功力不夠呢？！）

*利用一階濾波器的數學公式，我們可以輕易的調整其中的時間常數，與選用不同轉換速率的A/D ，

來符合我們系統應用的要求，這是真正的建立在科學數學基礎上的依據，而不是盲從的工程手法。

或是老闆或是賣MCU 業務的自由心證吧！

-------------------------------------------------
綜合以上的結論：您要採用哪一種作法，沒有人會管您，也不會說：哪一種作法有錯。

我只是要說：這一種是一個很非常簡單又常見的系統應用問題，

您去看市面上哪一本介紹單晶片MCU的書會跟您教這個 ？！

那怕他介紹的MCU 有A/D 他也不會提到這個。

據我所知：現在市面上小包裝、容量不到 1K 的MCU，也都有支援A/D 了，

所以這一種系統應用又更容易碰得到的。對您來說：又更容易發揮系統應用價值的。

或許您可以參考一下這樣的作法，也分享給各位。

-------------------------------------

------------------

-----
PS：這一部份的文章源自於過去鑽研引擎控制系統的經驗，他原始上在應用此一 Filter A/D 值時，

是拿來控制引擎的怠速控制回路的演算法，因為基本上，如果您有開車，也有留意到引擎怠速時，

您會發現：他就是一個Close Loop Control (閉迴路控制系統），他是採用所謂PID 控制原理，

他所擷取許多引擎外在環境參數都是經由此一Filter A/D 的作法，

所以，您會發現：您的引擎怠速控制時，

一下子冷氣壓縮機啟動、關閉，或是自動變速箱有變化，或是冷起啟動熱車時...等等，

您都會發現引擎轉速都會稍微上上下下的調整，又往往常常是路邊停車、引擎進入怠速狀態之後，

駕駛就會把小孩、家人留在車上，跑下車辦事情，所以，在引擎控制理論裡，

怠速控制絕對是一大研究議題的，所以他相對控制穩定性要求是很高的！

那您說：人家為什麼不採用簡單的讀十次取平均的作法，

幹嘛給自己添麻煩的搞了一個這麼複雜的工程數學的作法呢？！

或許是您我在研究這一個簡單系統應用案例時，一個簡單的可供思索的空間吧！

 

------------

1. 一個A/D 的系統應用問題

2.一個A/D 的系統應用問題（續篇-實驗結果）

3.一個A/D 的系統應用問題（續篇-精進版）